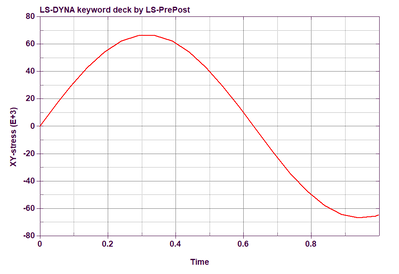
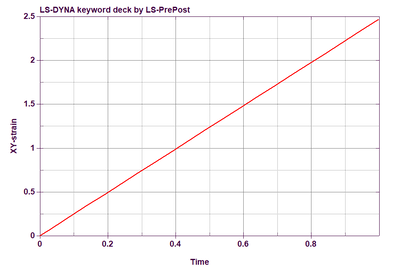
My question is regarding the calculation of the strain tensor in LS-prepost. Let's consider the problem of pure shear in a linearly elastic formulation (*MAT_ELASTIC). According to the material model, the shear components of stress and strain tensors should oscillate. Indeed, the shear components of the stress tensors (element time history) and elastic deformations (fringe component) oscillate, but the shear component of the strain tensor (element time history) is monotonous. To explain this paradox, it is necessary to understand how the strain tensor is calculated in LS-prepost. The Theory manual gives a confusing explanation without any formulas.
Let me help break this down. The apparent paradox you're observing between oscillating stress and monotonic strain in LS-DYNA's output requires understanding a few key concepts about how strains are calculated and reported.
In LS-DYNA, there are several different strain measures being calculated:
- The elastic strains (which you see oscillating in the fringe component)
- The total strain history (which you see as monotonic in the element time history)
- The rate of deformation tensor (which is used internally for calculations)
The key point is that the element time history typically shows the total accumulated strain (engineering strain), while the fringe component shows the instantaneous elastic strain. In a linear elastic material:
- The stress tensor is directly proportional to the elastic strain tensor through Hooke's law
- The elastic strains are recoverable deformations
- The total strain includes both elastic and any accumulated deformations
For pure shear in a linear elastic material:
- The stress (σ₁₂) oscillates as expected
- The elastic strain component (ε₁₂ᵉˡᵃˢᵗⁱᶜ) oscillates proportionally with stress
- The total strain (ε₁₂ᵗᵒᵗᵃˡ) accumulates over time
To verify this interpretation, you could:
- Plot both strain measures simultaneously to see their relationship
- Check the strain output formulation in your control cards
- Use the "STRFLG" parameter in *DATABASE_EXTENT_BINARY to control which strain measure is output
Thank you for your reply. Agree that such a difference in the interpretation of the strain tensor in a linear formulation is rather ridiculous. Moreover, the problem disappears immediately if we build a strain tensor by confrontational integration of the strain rate tensor (in the sense of Jaumann). The correctness of this approach is confirmed in LS-DYNA Theory Manual R14 (21.10 String Output to the LS-DYNA Database, formulas 21.54 - 21.57). Why this is not implemented in ls-prepost is completely unclear.
Also, make sure your version of LS-PrePost supports the version of LS-Dyna that you are running. The can be tricky when running newer revisions, especially since PrePost versions are basically a crap shoot between completely stable and a janky mess.